Chameleon hash function implementations

Chameleon Hash Function Implementations: Experimental setup and results

Setup:

The implementation is carried out on GNU/Linux (i486) platform with gcc-3.3.5, OpenSSL 0.9.7e library for cryptographic primitives (without any external cryptographic acceleration) and numerical analysis. To get a fair computational estimation, we did not use any code optimization of gcc while building our executables.

Approach to Compute Execution Time

Various approaches are possible to audit the process execution time. We employed the method of tracking CPU cycles consumed during execution of a function of our interest. The experiments are carried out on an AMD 750MHz machine, that complies IA32 architecture (which provides cycle counter; a 64-bit, unsigned number). The IA32 counter is accessed with the rdtsc (read time stamp counter) instruction. This instruction takes no arguments. It sets register %edx to the high-order 32 bits of the counter and register %eax to the low-order 32 bits. Based on this methodology, a pair of functions are integrated with our code that allows us to measure the total number of cycles that elapse between any two time points:

#include "clock.h"
void start_counter(); /* Starts the counter */
double get_counter(); /* Returns: Number of cycles since last call to start_counter */

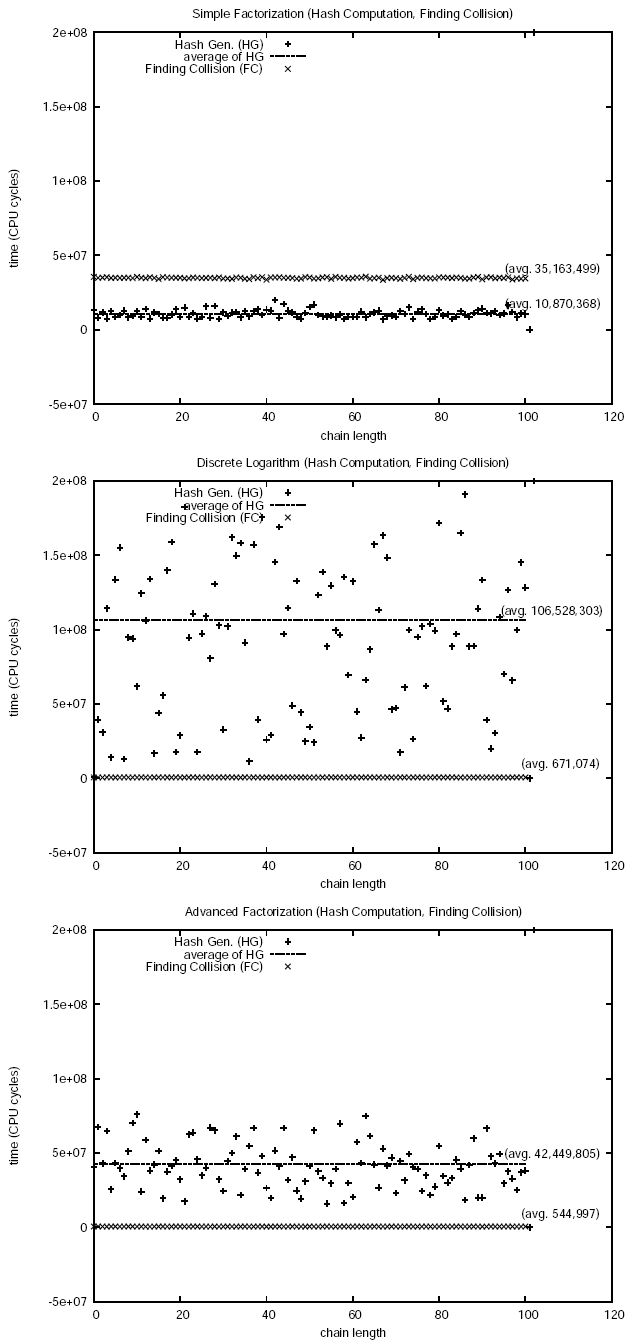
To verify the precision of this approach we marked the counter before and after sleep(sleeptime); function call (where sleeptime equals to one). We obtained 756,154,624.0 as return value (i.e., 756.2 MHz). We run each function of our interest for 101 times and discarded the first value of execution time in favor of cache warming process. Furthermore, results are gathered in run-level 1; to minimize interference from other processes. To plot all the results into graphs with common scale, we introduced dummy 101^st and 102^nd entries in our results with values equal to -1 and 200,000,000 respectively.

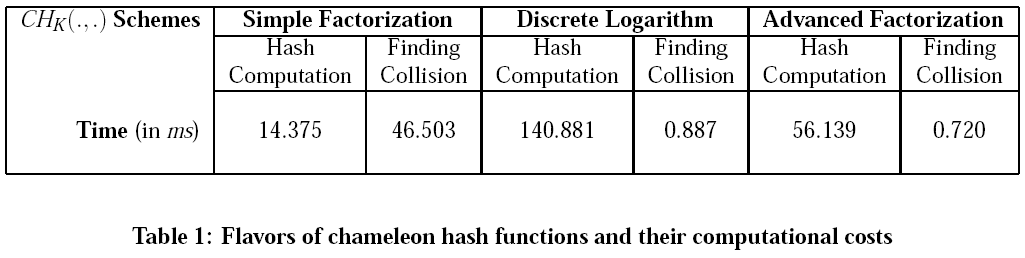
We implemented Chameleon scheme with three different methods, namely: Simple Factorization (SF), Discrete Logarithm (DL) [Chameleon Hashing and Signatures], and Advanced Factorization (AF) [Improved Online/Offline Signature Schemes]. Implementation of these schemes can be categorized into two phases: Hash Generation (HG) and Finding Collision (FC). These schemes produce hash of length 160-bits. Our results are summarized in the graphs shown in the Figure and Table shown below. The results provided in the following Table , for chameleon implementations, are the averages taken over 100 runs each.